T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
X
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
X
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
X
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
X
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
X
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
X
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
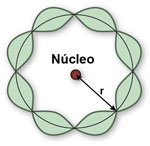
Propriedades ondulatórias das partículas
Em 1923, o físico francês Louis Victor de Broglie postulou o comportamento ondulatório da matéria:
"Em virtude de os fótons terem características ondulatórias e corpusculares, talvez todas as formas de matéria tenham propriedades ondulatórias e também corpusculares."
Esta foi uma ideia proposta, diferentemente das propostas por Thomson, Rutherford e Bohr, que não tinham evidências experimentais.
Este postulado diz que os elétrons têm também natureza dupla de partícula e onda, sendo acompanhados por uma onda.
Para a frequência f e o comprimento de onda λ da onda, associado ao elétron, ele propôs as equações
onde p é o momento e E a energia do elétron.
Note que a primeira equação é a de Planck, E=hf, para o fóton, agora utilizada para o elétron, e que a equação para λ também vale para
fótons e elétrons. Para os fótons temos que
Utilizando a relação entre energia e momento da relatividade especial, E=pc, temos:
As equações de Louis de Broglie foram propostas para qualquer tipo de matéria. Para corpos macroscópicos, os comprimentos de onda de Broglie são tão pequenos que impossibilitam a sua observação pela interferência ou pela difração. Calcule o comprimento de onda de uma partícula de massa 1g e velocidade 1.000 km/h.
Em 1927, experiências de difração realizadas com elétrons comprovaram as hipóteses de Louis de Broglie.
Função de onda
Com a comprovação experimental da natureza ondulatória das partículas, e estabelecido o seu comprimento de onda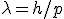 
, o próximo passo foi descobrir qual grandeza física está associada à onda de matéria. Nenhuma grandeza física conhecida explica a natureza dessas ondas, então foi utilizada a letra grega Ψ para designar a função de onda da matéria.
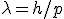, o próximo passo foi descobrir qual grandeza física está associada à onda de matéria. Nenhuma grandeza física conhecida explica a natureza dessas ondas, então foi utilizada a letra grega Ψ para designar a função de onda da matéria.
Em 1926, Erwin Schrödinger descobriu uma equação que permite encontrar a função de onda de uma partícula, a partir do conhecimento da energia potencial à qual esta está submetida.
Entretanto foi Max Born que, em 1928, descobriu a relação entre a função de onda e a probabilidade de se encontrar a partícula numa determinada posição. Ele concluiu que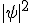 
é a grandeza estatística que representa a densidade de probabilidade. Esta função dá a probabilidade de encontrarmos uma partícula numa determinada região do espaço.
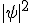é a grandeza estatística que representa a densidade de probabilidade. Esta função dá a probabilidade de encontrarmos uma partícula numa determinada região do espaço.
Com esta última descoberta, a Física Quântica mostra que a natureza possui um comportamento estatístico, sendo descrita por uma função que representa a probabilidade. Este fato incomodou muitos físicos, inclusive Einstein, que expressou sua insatisfação dizendo:
- Deus não joga dados com o Universo.
Entretanto os resultados experimentais dão o veredicto a favor da formulação quântica.
Equação de Schrödinger
A Equação de Schrödinger permite calcular a função de onda Ψ (r,t), associada a uma partícula que se move dentro de um campo de forças descrito por um potencial V (r,t). No caso em que o potencial não depende do tempo, ela é expressa do seguinte modo:
A resolução da Equação de Schrödinger conduz a um conjunto de funções de onda e a um conjunto de energias correspondentes aos estados do elétron permitidos no átomo. As expressões matemáticas das funções de onda possibilitam determinar a probabilidade de encontrar o elétron na vizinhança de um ponto próximo do núcleo.
No caso do átomo de hidrogênio, a energia potencial eletrostática é dada por
onde e é a carga elementar, εo é a constante elétrica de permissividade no vácuo e r é a distância ao centro do átomo. Este é um potencial no espaço tridimensional.
Energias do hidrogênio
A solução da Equação de Schrödinger para este potencial, que não apresentarei aqui, mostra que os valores de energia são quantizados, e são os mesmos obtidos pelo modelo de Bohr.
